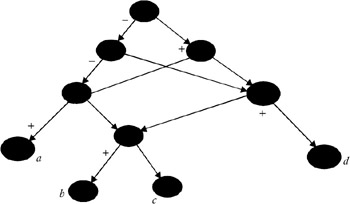
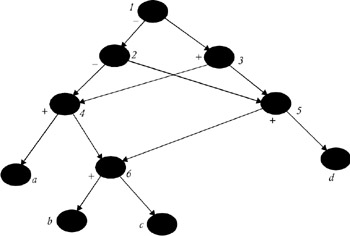
To rearrange the final computation order for more-efficient code-generation, we first obtain a DAG representation of the basic block, and then we order the nodes of the DAG using heuristics. Heuristics attempts to order the nodes of a DAG so that, if possible, a node immediately follows the evaluation of its left-most operand.
1 Heuristic DAG Ordering
The algorithm for heuristic ordering is given below. It lists the nodes of a DAG such that the node’s reverse listing results in the computation order.
{
While there exists an unlisted interior node do
{
select an unlisted node n whose parents have been listed
list n
while there exists a left-most child m of n that has no
unlisted parents and m is not a leaf do
{
list m
m = n
}
}
order = reverse of the order of listing of nodes
}
The order in which the nodes are listed by the heuristic ordering is shown in Figure 2.
Therefore, the computation order is:

If the DAG representation turns out to be a tree, then for the machine model described above, we can obtain the optimal order using the algorithm described in Section 2, below. Here, an optimal order means the order that yields the shortest instruction sequence.
2 The Labeling Algorithm
This algorithm works on the tree representation of a sequence of three-address statements. It could also be made to work if the intermediate code form was a parse tree. This algorithm has two parts: the first part labels each node of the tree from the bottom up, with an integer that denotes the minimum number of registers required to evaluate the tree and with no storing of intermediate results. The second part of the algorithm is a tree traversal that travels the tree in an order governed by the computed labels in the first part, and which generates the code during the tree traversal.
{
if n is a leaf node then
if n is the left-most child of its parent then
label(n) = 1
else
label(n) = 0
else
label(n) = max[label(ni) + (i - 1)]
for i = 1 to k
/* where n1, n2,..., nk are the children of n, ordered by their labels; that is,
label(n1) ≥ label(n2) ≥ ... ≥ label(nk) */
}
For k = 2, the formula label(n) = max[label(ni) + (i - 1)] becomes:
label(n) = max[11, 12 + 1]
where 11 is label(n1), and 12 is label(n2). Since either 11 or 12 will be same, or since there will be a difference of at least the difference between 11 and 12 (i.e., 11 − 12), which is greater than or equal to one, we get:
![]()
Figure 3: DAG representation of three-address code for Example 2.
3 Code Generation by Traversing the Labeled Tree
We will now examine an algorithm that traverses the labeled tree and generates machine code to evaluate the tree in the register R0. The content of R0 can then be stored in the appropriate memory location. We assume that only binary operators are used in the tree. The algorithm uses a recursive procedure, gencode(n), to generate the code for evaluating into a register a subtree that has its root in node n. This procedure makes use of RSTACK to allocate registers.
Initially, RSTACK contains all available registers. We assume the order of the registers to be R0, R1,…, from top to bottom. A call to gencode() may find a subset of registers, perhaps in a different order in RSTACK, but when gencode() returns, it leaves the registers in RSTACK in the same order in which they were found. The resulting code computes the value of the tree in the top register of RSTACK. It also makes use of TSTACK to allocate temporary memory locations. Depending upon the type of node n with which gencode() is called, gencode() performs the following:
-
If n is a leaf node and is the left-most child of its parent, then gencode() generates a load instruction for loading the top register of RSTACK by the label of node n:

-
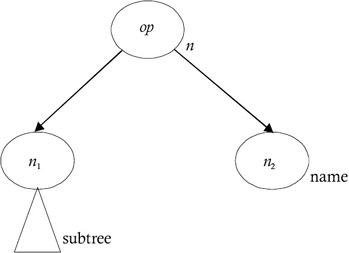
If n is an interior node, it will be an operator node labeled by op with the children n1 and n2, and n2 is a simple operand and not a root of the subtree, as shown in Figure 5.

Figure 5: The node n is an operand and not a subtree root.In this case, gencode() will first generate the code to evaluate the subtree rooted at n1 in the top{RSTACK]. It will then generate the instruction, OP name, RSTACK[top].
-
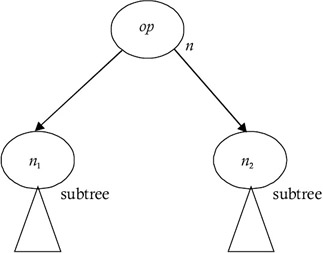
If n is an interior node, it will be an operator node labeled by op with the children n1 and n2, and both n1 and n2 are roots of subtrees, as shown in Figure 6.

Figure 6: The node n is an operator, and n1 and n2 are subtree roots.In this case, gencode() examines the labels of n1 and n2. If label(n2) > label(n1), then n2 requires a greater number of registers to evaluate without storing the intermediate results than n1 does. Therefore, gencode() checks whether the total number of registers available to r is greater than the label(n1). If it is, then the subtree rooted at n1 can be evaluated without storing the intermediate results. It first swaps the top two registers of RSTACK, then generates the code for evaluating the subtree rooted at n2, which is harder to evaluate in RSTACK[top]. It removes the top-most register from RSTACK and stores it in R, then generates code for evaluating the subtree rooted at n1 in RSTACK[top]. An instruction, OP R, RSTACK[top], is generated, pushing R onto RSTACK. The top two registers are swapped so that the register holding the value of n will be in the top register of RSTACK.
-
If label(n2) <= label(n1), then n1 requires a greater number of register to evaluate without storing the intermediate results than n2 does. Therefore, gencode() checks whether the total number of registers available to r is greater than label(n2). If it is, then the subtree rooted at n2 can be evaluated without storing the intermediate results. Hence, it first generates the code for evaluating subtree rooted at n1, which is harder to evaluate in RSTACK[top], removes the top-most register from RSTACK, and stores it in R. It then generates code for evaluating the subtree rooted at n2 in RSTACK[top]. An instruction, OP RSTACK[top], R, is generated that pushes register R onto RSTACK. In this case, the top register, after pushing R onto RSTACK, holds the value of n. Therefore, swapping and reswapping is needed.
-
If label(n1) as well as label(n2) are greater than or equal to r (i.e., both subtrees require r or more registers to evaluate without intermediate storage), a temporary memory location is required. In this case, gencode() first generates the code for evaluating n2 in a temporary memory location, then generates code to evaluate n1, followed by an instruction to evaluate root n in the top register of RSTACK.
Algorithm for Implementing Gencode()
The procedure for gencode() is outlined as follows:
Procedure gencode(n)
{
if n is a leaf node and the left-most child of its parent then
generate MOV name, RSTACK[top]
if n is an interior node with children n1 and n2, with
label(n2) = 0 then
{
gencode(n1)
generate op name RSTACK[top] /* name is the operand
represented by n2 and op is the operator
represented by n*/
}
if n is an interior node with children n1 and n2,
label(n2) > label(n1), and label(n1) < r then
{
swap top two registers of RSTACK
gencode(n2)
R = pop(RSTACK)
gencode(n1)
generate op R, RSTACK[top] /* op is the operator
represented by n */
PUSH(R,RSTACK)
swap top two registers of RSTACK
}
if n is an interior node with children n1 and n2,
label(n2) <= label(n1), and label(n2) < r then
{
gencode(n1)
R = pop(RSTACK)
gencode(n2)
generate op RSTACK[top], R /* op is the operator
represented by n */
PUSH(R, RSTACK)
}
if n is an interior node with children n1 and n2,
label(n2) <= label(n1), and label(n1) > r as well as
label(n2) > r then
{
gencode(n2)
T = pop(TSTACK)
generate MOV RSTACK[top], T
gencode(n1)
PUSH(T, TSTACK)
generate op T, RSTACK[top] /* op is the operator
represented by n */
}
}
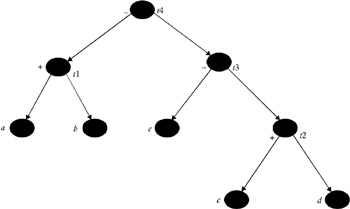
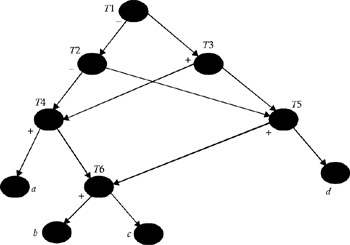
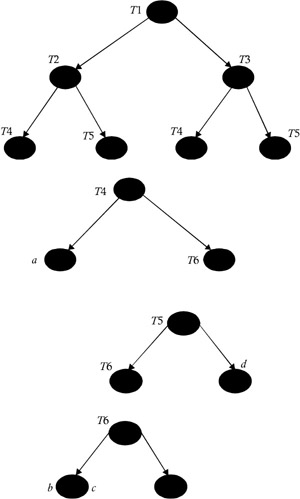
The algorithm above can be used when the DAG represented is a tree; but when there are common subexpressions in the basic block, the DAG representation will no longer be a tree, because the common subexpressions will correspond to nodes with more than one parent. These are called “shared nodes”. In this case, we can apply the labeling and the gencode() algorithm by partitioning the DAG into a set of trees. We find, for each shared node as well as root n, the maximal subtree with n as a root that includes no other shared nodes, except as leaves. For example, consider the DAG shown in Figure 7. It is not a tree, but it can be partitioned into the set of trees shown in Figure 8. The procedure gencode() can be used to generate code for each node of this tree.
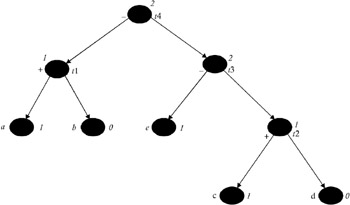
Figure 9: Labeled tree for Example 3.
The code generated by gencode() when this tree is given as input along with the recursive calls of gencode is shown in Table 1. It starts with call to gencode() of t4. Initially, the top two registers will be R0 and R1.
|
Call to Gencode() |
Action Taken |
RSTACK Contents Top Two Registers |
Code Generated |
|---|---|---|---|
| � | � |
R0, R1 |
� |
|
gencode(t4) |
Swap top two registers Call gencode(t3) Pop R1 Call gencode(t1) Generate an instruction SUB R1,R0 Push R1 Swap top two registers |
R1, R0 R1, R0 |
MOV E, R1 |
|
gencode(t3) |
Call gencode(E) Pop R1 Call gencode(t2) Generate an instruction SUB R0,R1 Push R1 |
R1, R0 R0 R1, R0 |
MOV E, R1 |
|
gencode(E) |
Generate an instruction MOV E, R1 |
R1, R0 |
MOV E, R1 |
|
gencode(t2) |
gencode(c) Generate an instruction ADD D, R0 |
R0 |
MOV C, R0 |
|
gencode(c) |
Generate an instruction MOV C, R0 |
R0 |
� |
|
gencode(t1) |
gencode(A) Generate an instruction ADD B, R0 |
R0 |
MOV A, R0 |
|
gencode(A) |
Generate an instruction MOV A, R0 |
R0 |
MOV A, R0 |