Bias in the Estimate
The main purpose of inferential statistics, is to infer population parameters such as μ and σ from sample statistics such as 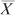 and s. You will sometimes see
and s. You will sometimes see 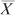 and s and other statistics referred to as estimators, particularly in the context of inferring population values.
and s and other statistics referred to as estimators, particularly in the context of inferring population values.
Estimators have several desirable characteristics, and one of them is unbiasedness. The absence of bias in a statistic that’s being used as an estimator is desirable. The mean is an unbiased estimator. No special adjustment is needed for 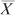 to estimate μ accurately.
to estimate μ accurately.
But when you use N, instead of the N − 1 degrees of freedom, in the calculation of the variance, you are biasing the statistic as an estimator. It is then biased negatively: it’s an underestimate of the variance in the population.
As discussed in the prior section, that’s the reason to use the degrees of freedom instead of the actual sample size when you infer the population variance from the sample variance. So doing removes the bias from the estimator.
It’s easy to conclude, then, that using N − 1 in the denominator of the standard deviation also removes its bias as an estimator of the population standard deviation. But it doesn’t. The square root of an unbiased estimator is not itself necessarily unbiased.
Much of the bias in the standard deviation is in fact removed by the use of the degrees of freedom instead of N in the denominator. But a little is left, and it’s usually regarded as negligible.
The larger the sample size, of course, the smaller the correction involved in using the degrees of freedom. With a sample of 100 values, the difference between dividing by 100 and dividing by 99 is quite small. With a sample of ten values, the difference between dividing by 10 and dividing by 9 can be meaningful.
Similarly, the degree of bias that remains in the standard deviation is very small when the degrees of freedom instead of the sample size is used in the denominator. The standard deviation remains a biased estimator, but the bias is only about 1% when the sample size is as small as 20, and the remaining bias becomes smaller yet as the sample size increases.
Note
You can estimate the bias in the standard deviation as an estimator of the population standard deviation that remains after the degrees of freedom has replaced the sample size in the denominator. In a normal distribution, this expression is an unbiased estimator of the population standard deviation:
(1 + 1 / [4 * {n – 1}]) * s
Degrees of Freedom
The concept of degrees of freedom is important to calculating variances and standard deviations. But as you move from descriptive statistics to inferential statistics, you encounter the concept more and more often. Any inferential analysis, from a simple t-test to a complicated multivariate linear regression, uses degrees of freedom (df) as part of the math and to help evaluate how reliable a result might be. The concept of degrees of freedom is also important for understanding standard deviations, as the prior section discussed.
Unfortunately, degrees of freedom is not a straightforward concept. It’s usual for people to take longer than they expect to become comfortable with it.
Fundamentally, degrees of freedom refers to the number of values that are free to vary. It is often true that one or more values in a set are constrained. The remaining values—the number of values in that set that are unconstrained—constitute the degrees of freedom.
Consider the mean of three values. Once you have calculated the mean and stick to it, it acts as a constraint. You can then set two of the three values to any two numbers you want, but the third value is constrained by the calculated mean.
Take 6, 8, and 10. Their mean is 8. Two of them are free to vary, and you could change 6 to 2 and 8 to 24. But because the mean acts as a constraint, the original 10 is constrained to become −2 if the mean of 8 is to be maintained.
When you calculate the deviation of each observation from the mean, you are imposing a constraint—the calculated mean—on the values in the sample. All of the observations but one (that is, N − 1 of the values) are free to vary, and with them the sum of the squared deviations. One of the observations is forced to take on a particular value, in order to retain the value of the mean.
Excel’s Variability Functions
The 2010 version of Excel reorganizes and renames several statistical functions. The aim is to name the functions according to a more consistent pattern, and to make a function’s purpose more apparent from its name.
Standard Deviation Functions
For example, Excel has since 1995 offered two functions that return the standard deviation:
-
STDEV() —This function assumes that its argument list is a sample from a population, and therefore uses N − 1 in the denominator.
-
STDEVP() —This function assumes that its argument list is the population, and therefore uses N in the denominator.
In its 2003 version, Excel added two more functions that return the standard deviation:
-
STDEVA() —This function works like STDEV() except that it accepts alphabetic, text values in its argument list and also Boolean (TRUE or FALSE) values. Text values and FALSE values are treated as zeroes, and TRUE values are treated as ones.
-
STDEVPA() —This function accepts text and Boolean values, just as does STDEVA(), but again it assumes that the argument list constitutes a population.
Microsoft decided that using P, for population, at the end of the function name STDEVP() was inconsistent because there was no STDEVS(). That would never do, and to remedy the situation, Excel 2010 includes two new standard deviation functions that append a letter to the function name in order to tell you whether it’s intended for use with a sample or on a population:
-
STDEV.S() —This function works just like STDEV—it ignores Boolean values and text.
-
STDEV.P() —This function works just like STDEVP—it also ignores Boolean values and text.
STDEV.S() and STDEV.P() are termed consistency functions because they introduce a new, more consistent naming convention than the earlier versions. Microsoft also states that their computation algorithms bring about more accurate results than is the case with STDEV() and STDEVP().
Excel 2010 continues to support the old STDEV() and STDEVP() functions, although it is not at present clear how long they will continue to be supported. In recognition of their deprecated status, STDEV() and STDEVP() occupy the bottom of the list of functions that appears in a pop-up window when you begin to type =STD in a worksheet cell. Excel 2010 refers to them as compatibility functions.
Variance Functions
Similar considerations apply to the worksheet functions that return the variance. The function’s name is used to indicate whether it is intended for a population or to infer a population value from a sample, and whether it can deal with nonnumeric values in its arguments.
-
VAR() has been available in Excel since its earliest versions. It returns an unbiased estimate of a population variance based on values from a sample and uses degrees of freedom in the denominator. It is the square of STDEV().
-
VARP() has been available in Excel for as long as VAR(). It returns the variance of a population and uses the number of records, not the degrees of freedom, in the denominator. It is the square of STDEVP().
-
VARA() made its first appearance in Excel 2003. See the discussion of STDEVA(), for the difference between VAR() and VARA().
-
VARPA() also first appeared in Excel 2003 and takes the same approach to its nonnumeric arguments as does STDEVPA().
-
VAR.S() is new in Excel 2010. Microsoft states that its computations are more accurate than are those used by VAR(). Its use and intent is the same as VAR().
-
VAR.P() is new in Excel 2010. Its similarities to VARP() are analogous to those between VAR() and VAR.S().